Combinatorics is the study of finite and discrete structures. Starting from fundamental questions of ordering, decomposition and structuring of finitely many objects or states, combinatorics represents the nanotechnology of mathematics and its applications. Due to its interdisciplinarity, it is a central mathematical research area with influence across disciplinary boundaries. Questions are unified and sound theories with intrinsic questions and methods are developed from structurally related approaches. The two 2022 Fields Medals to June Huh and Maryna Viazovska for solutions to central combinatorial problems emphasizes both the importance and timeliness as well as the potential of this field.

What is this priority programme about?

Discrete data has always been a source for the development of mathematical theories. Their analysis is comparable to the derivation of physical laws from observations of phenomena in nature. Due to the complexity of mathematical observations we are at the beginning of a revolution for the development cycles in the interplay of data and structure. This change in research methodology is being met worldwide with versatile programmes focused on combinatorics.

We see the emerging opportunities as a chance and we aim at shaping these opportunities in Germany with this priority programme SPP 2458 Combinatorial synergies. As a community, we plan to create a combinatorics network that establishes innovative methods and enhances the field of combinatorics as a cross-cut technology.

The awareness of big data already existist in the individual working groups will become a worldleading feature of this network.

This priority programme links the huge potential of excellent and dynamic combinatorics groups. It will enable breakthrough advances within and across the thematic areas. In the process, the accessibility and usability of discrete data will act as a multiplier. A globally visible combinatorics network in modern basic mathematical research will be created.

What are the nine themes of the programme?

We identify nine themes that represent combinatorics as a cross-cutting field and will particularly benefit from the changing development cycles:

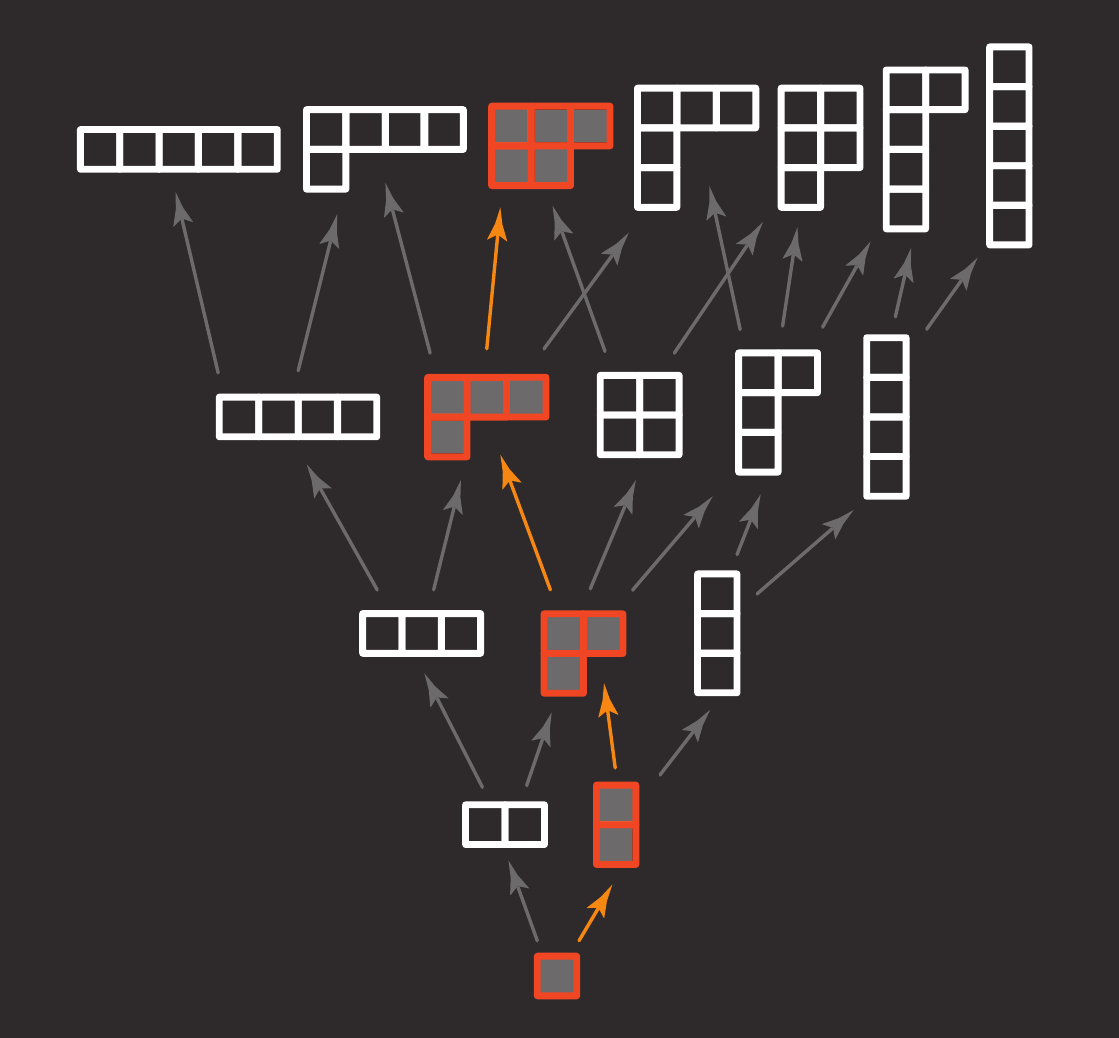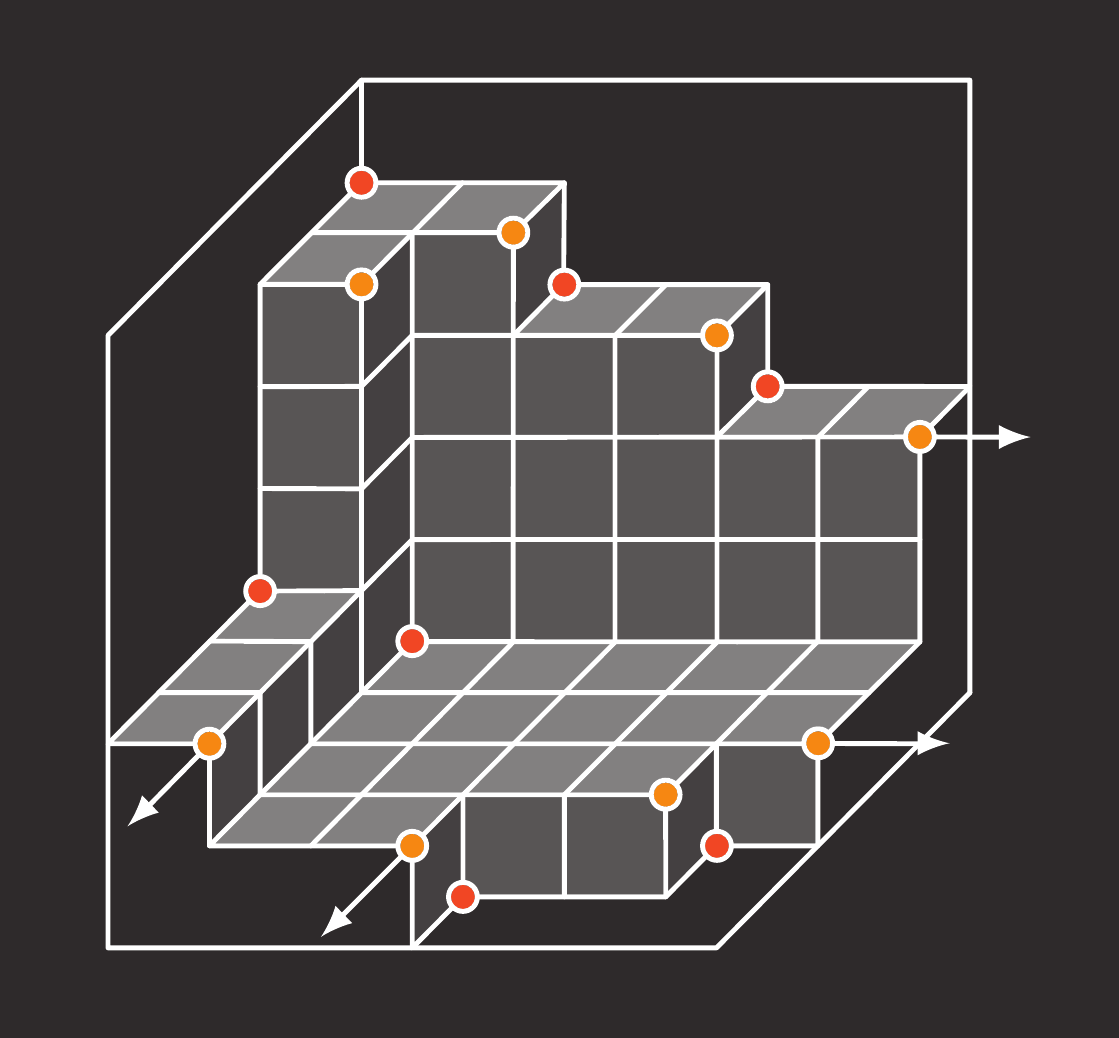Enumeration	Dynkin Classification	Commutative Algebra
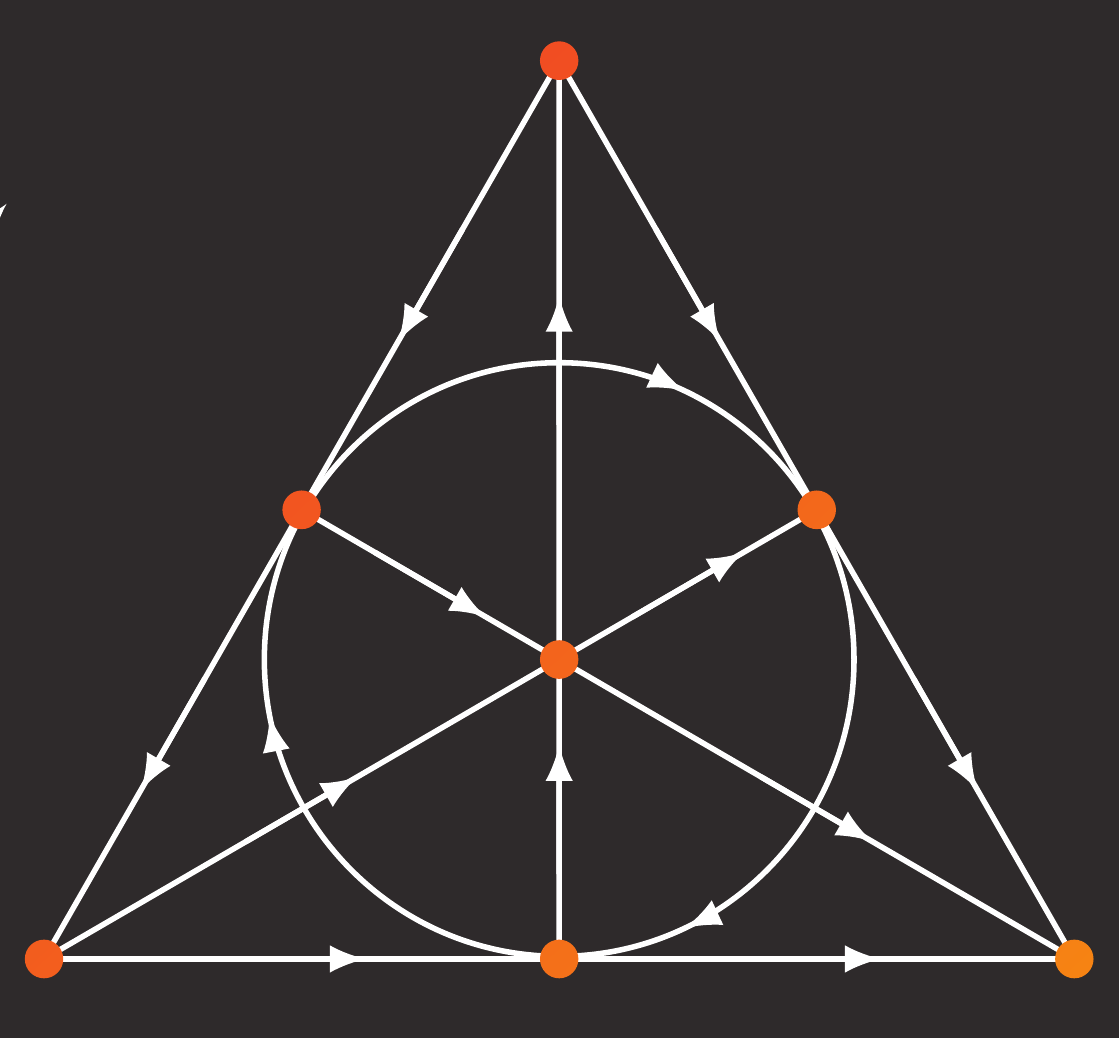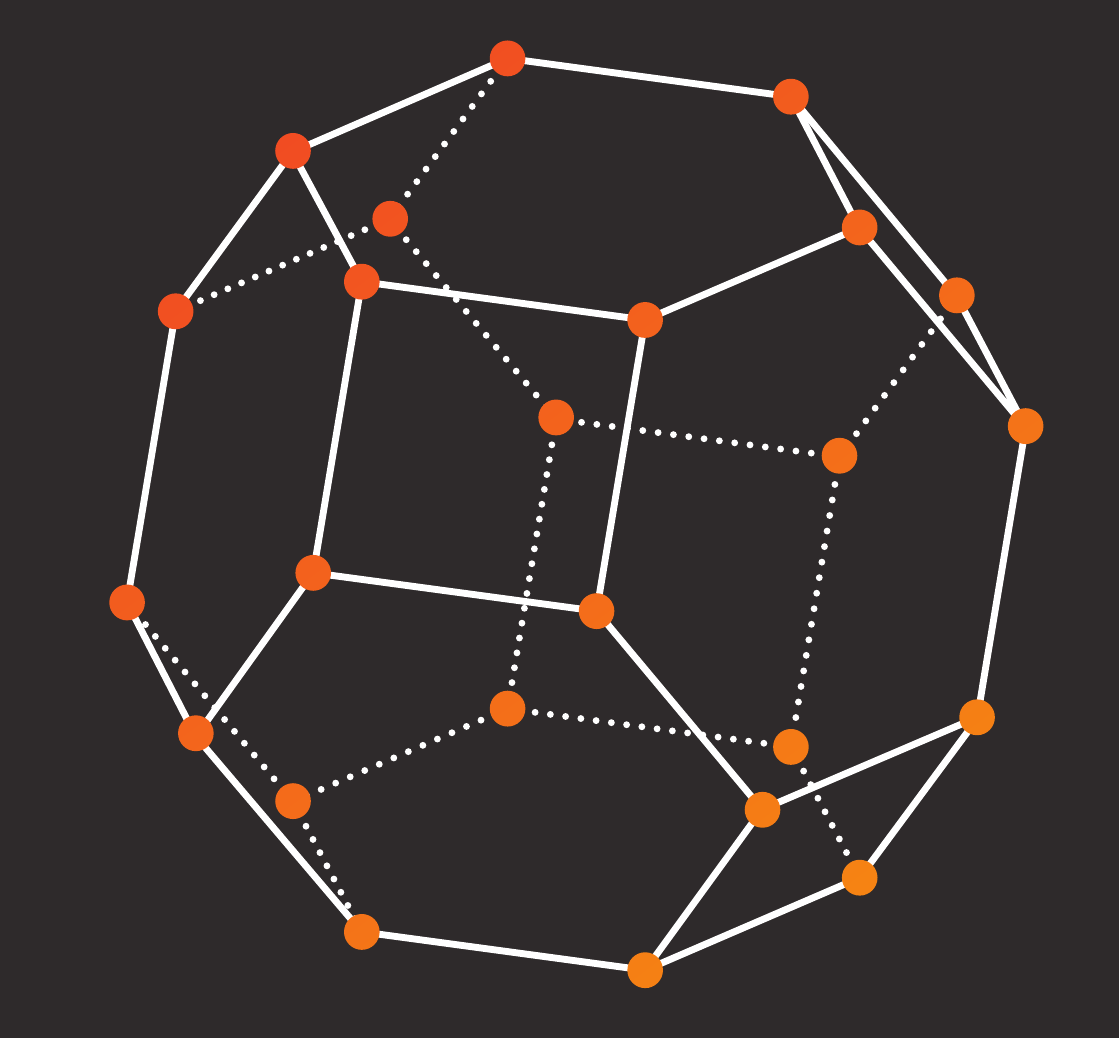Matroids	Convexity	Lattice Points
Statistics	Non-linear Optimization	Mathematical Physics

These concern fundamental mathematical research in its breadth and related application areas. We identify the existing potential in Germany as well as future-oriented leading questions and synergies in the interplay of the complex of topics.